- 貨架第三方檢測-CNAS/CMA/SEMA三重資質認可認定
- phone021-67157048
- recent_actors
職業責任險 - bubble_chart
產品責任險 - security
公正性聲明 - gavel
侵權聲明
- event2021-11-20 13:40:55
- person 穩圖WESAFE
- local_library 原創
- visibility 閱讀:437
構件設計承載力應通過測試或理論計算方法確定。理論計算方法應合理考慮開孔與局部屈曲、整體屈曲和畸變屈曲以及缺陷的相互作用影響。對于連續開孔的構件,理論計算方法應通過測試驗證。
連續開孔構件的設計需要測試,但是并不限制理論計算方法(比如有限元法)應用于開孔或無孔構件的計算。
一、截面校核
均勻受壓的立柱,應滿足:
NEd≤Nc,Rd
其中
NEd為設計軸壓力;
Nc,Rd=fyAeff/γM1
Aeff為均勻受壓截面的有效面積。
二、彎曲屈曲
彎曲屈曲承載力應按下式確定:
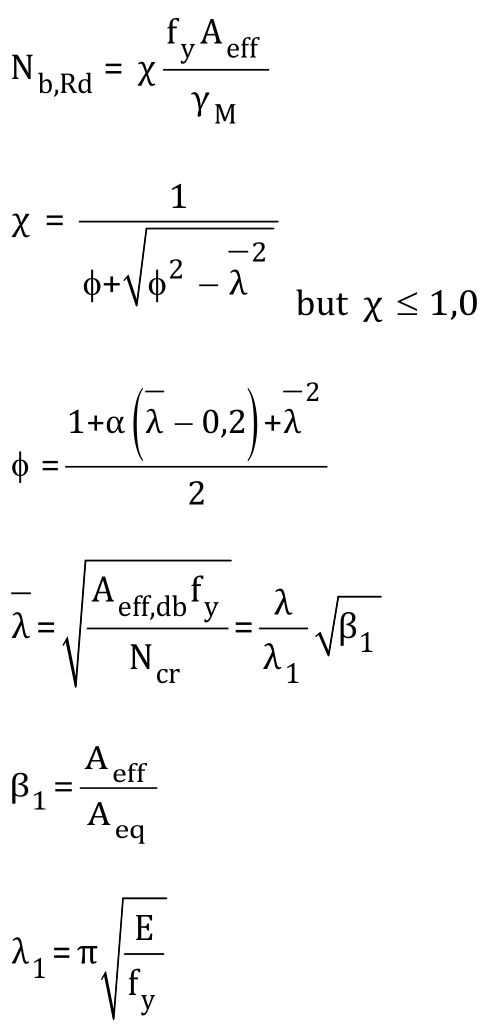
其中
Ncr為等效截面的立柱發生彎曲屈曲的彈性臨界軸力
Aeff為考慮局部屈曲Aeff,lb與畸變屈曲Aeff,db的較小值
Aeq為等效截面積
λ為長細比,對于彎曲屈曲,λy=ly/ieq,y,λz=lz/ieq,z
l為屈曲長度
ieq等效截面回轉半徑
α為缺陷系數,見表1。
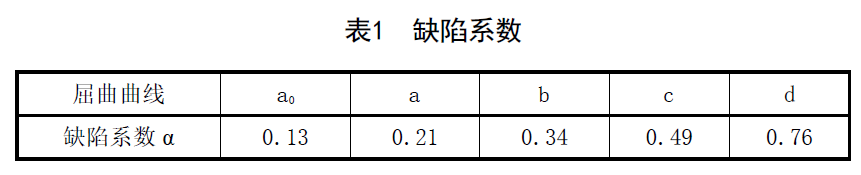
2.1 屈曲曲線
圖1 屈曲曲線
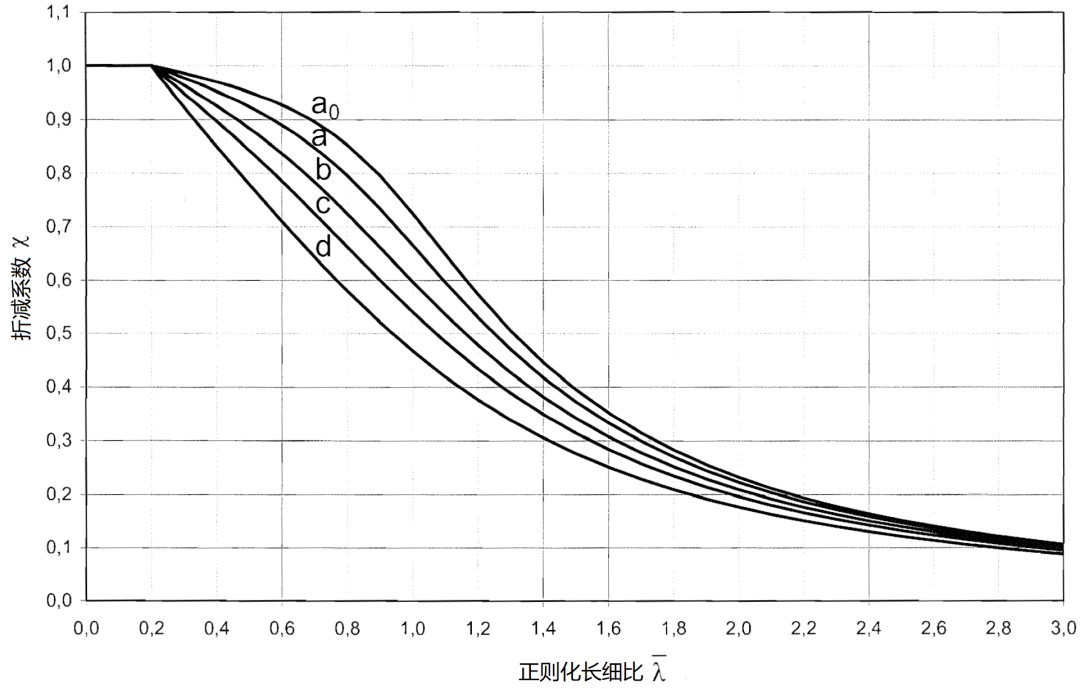
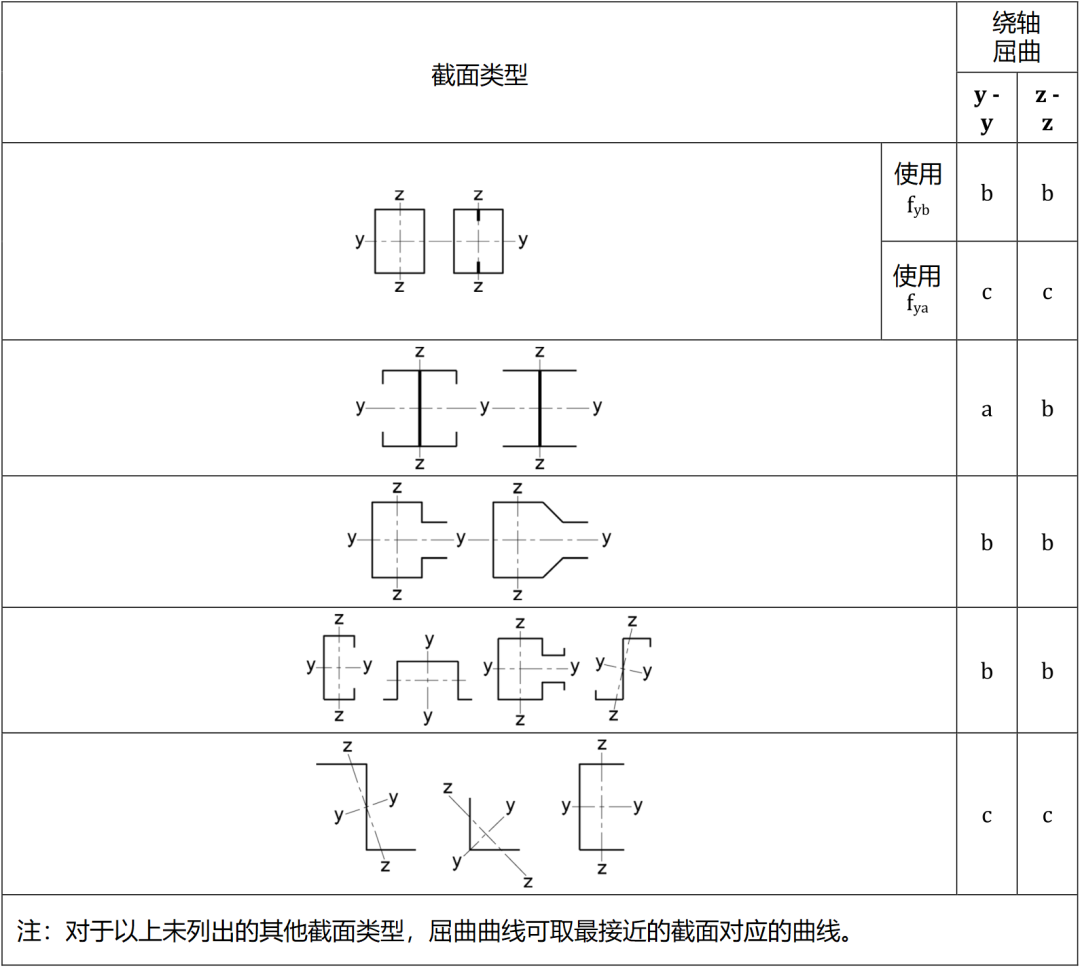
屈曲曲線的選擇,取決于截面類型與屈曲平面。每條屈曲曲線對應一個缺陷系數α值。特定截面對應的恰當屈曲曲線應根據表2確定。
表2 不同冷成型截面類型屈曲曲線
2.2 彎曲屈曲長度
彎曲屈曲長度l:
l=KL
其中
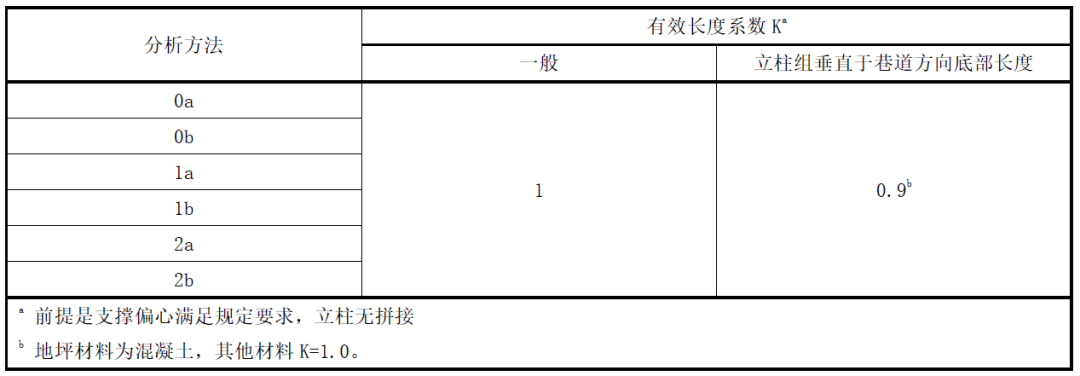
K為有效長度系數,對于無支撐貨架比較復雜需要專門分析確定,對于有支撐貨架見表3;
L為體系長度,見圖2、圖3與圖6。
表3 有效長度系數K
當最底部支撐以下的立柱不滿足支撐偏心要求時,地坪與第一支撐點之間的立柱長度應視為是可以自由側移的。對于圖2c)所示的頂部無支撐部分立柱,應按無支撐貨架確定相應的有效長度。
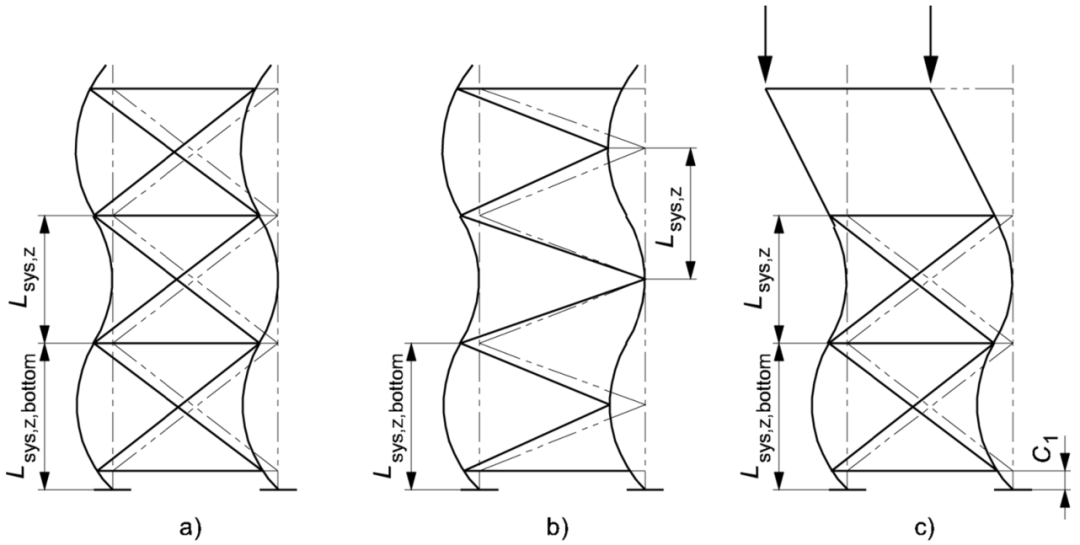
C1為地坪與最底部第一支撐點之間的立柱長度
Lsys,z,bottom為地坪與底部第二支撐點之間的立柱長度
Lsys,z為步距
圖2 立柱組面內屈曲模式
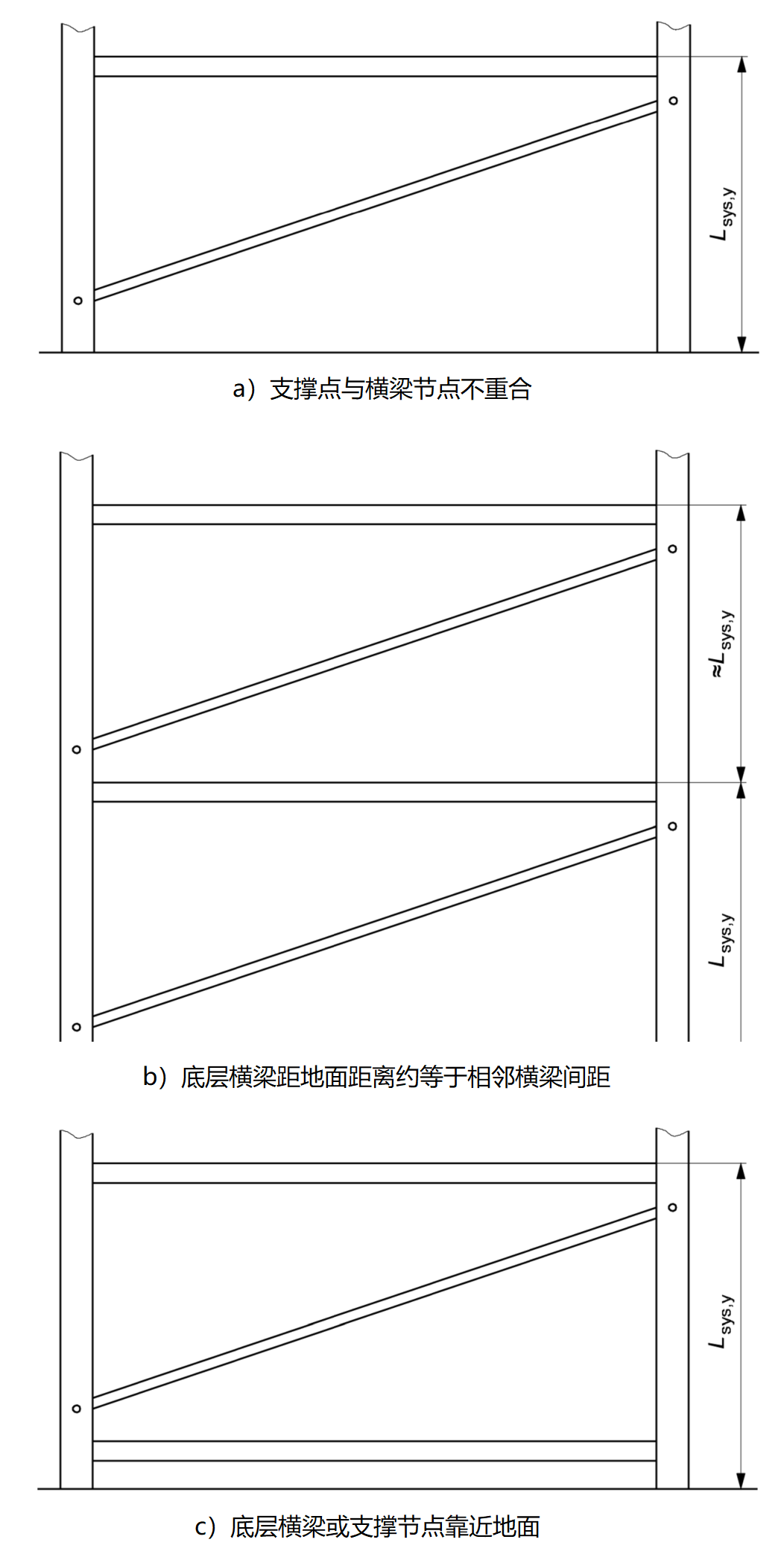
圖3 沿巷道方向有支撐的貨架
三、扭轉屈曲或彎扭屈曲
扭轉或彎扭屈曲承載力應用Ncr,T和Ncr,TF的較小值代替彎曲屈曲的Ncr:
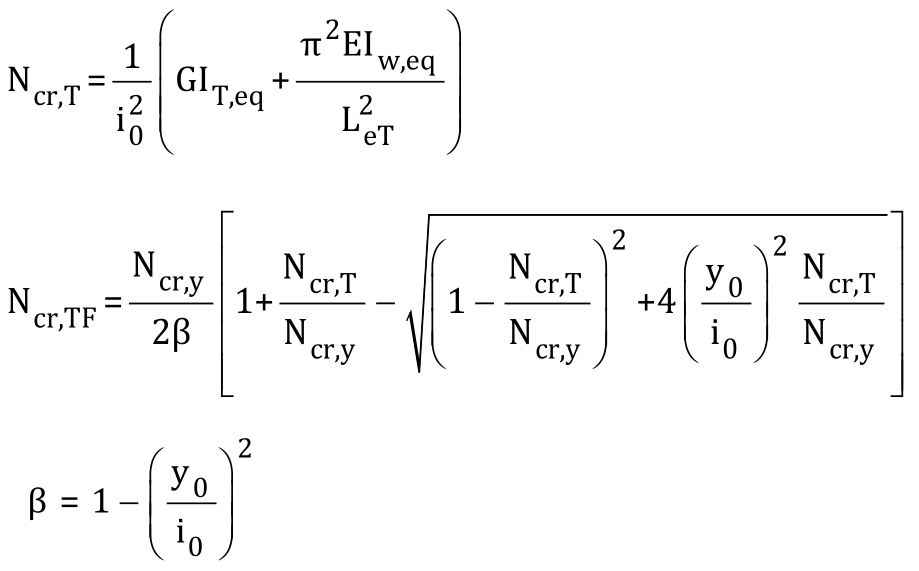
其中
y-y軸為對稱軸
Ncr,TF為彎曲屈曲臨界荷載
Ncr,T為扭轉屈曲臨界荷載
Ncy,y繞y-y軸彎曲屈曲臨界荷載
i02=ieq,y2+ieq,z2+yeq,02
yeq,0為等效截面剪心到形心沿y軸方向的距離
LeT為扭轉屈曲長度
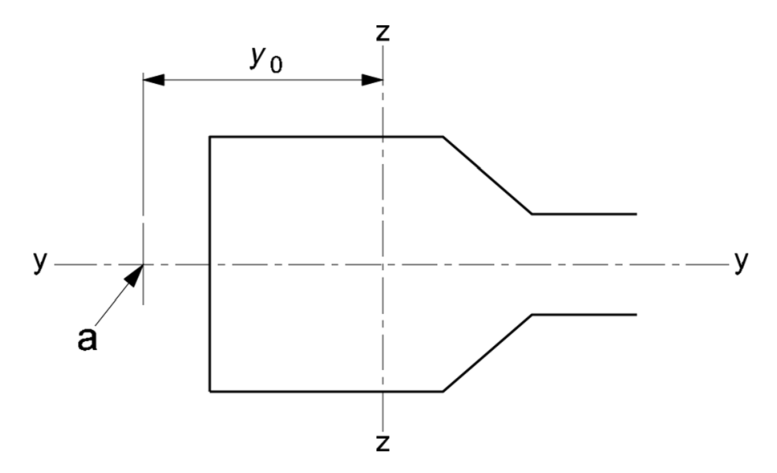
圖4 剪心位置
3.1 扭轉屈曲長度
扭轉屈曲長度lT:
lT=KTLeq
其中
KT見表4;
Leq為等效步距,見表5。
表4有效長度系數KT
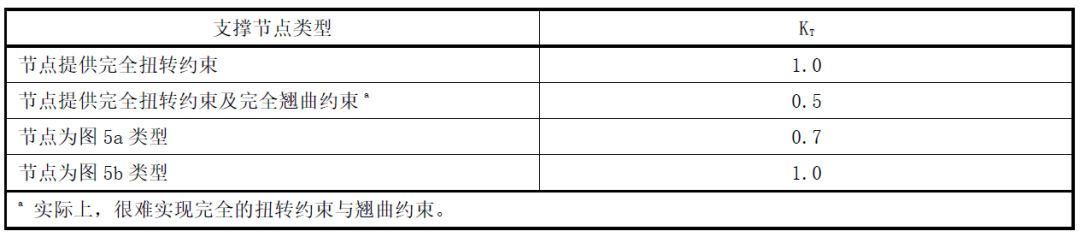
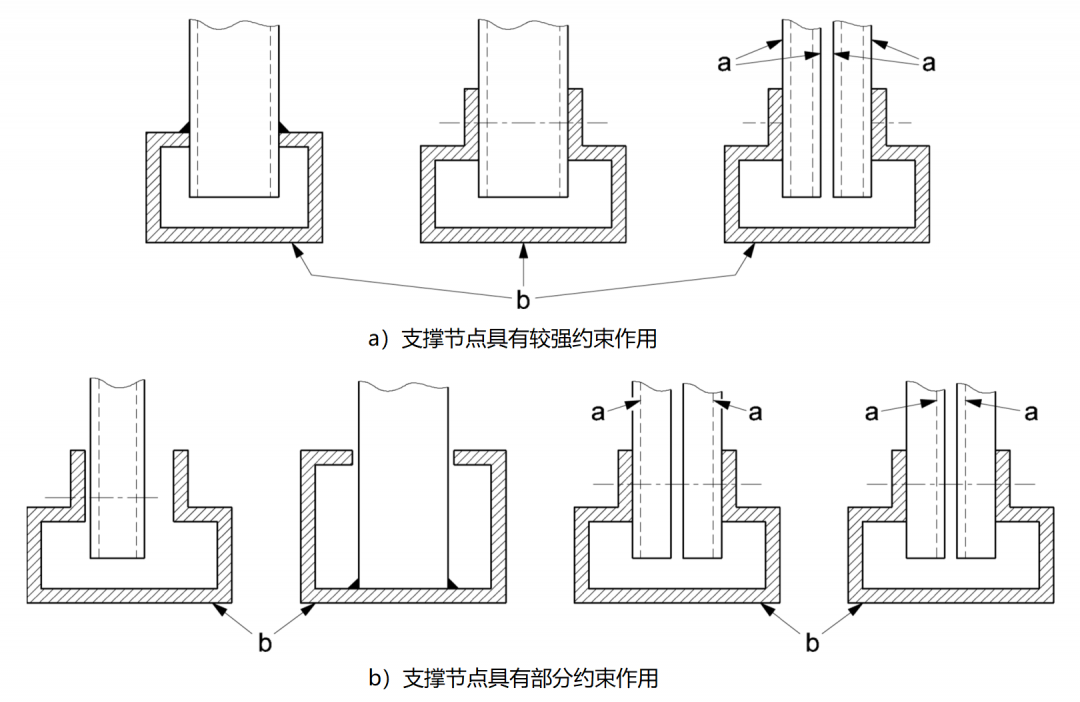
a (圖5a)每根支撐構件的兩面腹板通過螺栓與立柱連接
a (圖5b)每根支撐構件僅有一面腹板通過螺栓與立柱連接
b 立柱
圖5 支撐節點示列
表5 等效步距

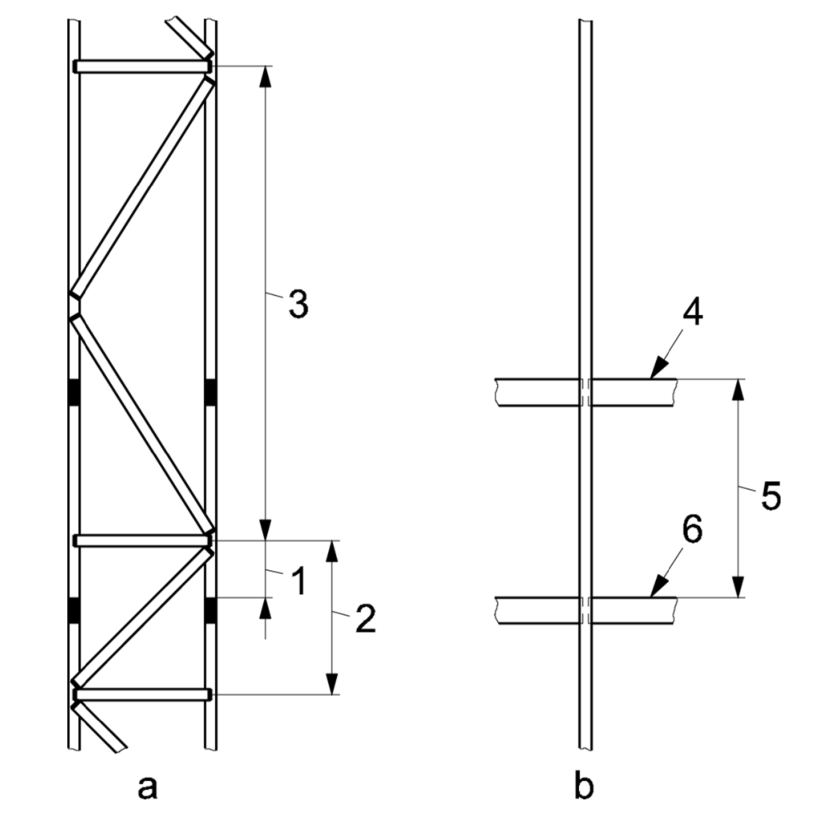
1 α×Lsys;y;i+1
2 Lsys;z;i
3 Lsys;z;i+1
4 第i+1層橫梁
5 Lsys;y;i+1
6 第i層橫梁
a YZ平面
b YX平面
圖6 體系長度
四、壓彎組合
4.1 壓彎截面承載力
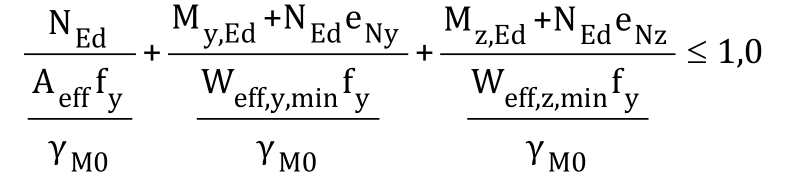
其中
Aeff為均勻受壓時的有效截面積
Weff,min為僅受彎時的有效截面模量(對應邊緣纖維最大彈性應力)
eN為有效截面形心相對于毛截面形心的偏移。
4.2 壓彎構件屈曲承載力
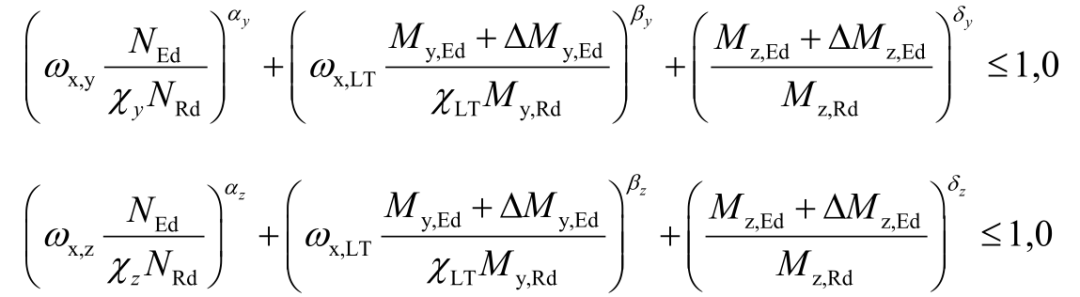
其中
NEd為軸壓力設計值(見圖7)
My,Ed,Mz,Ed為彎矩設計值(見圖7),或保守地取端彎矩最大值。
ΔMy,Ed,ΔMz,Ed為有效截面形心相對于毛截面形心的偏移引起的附加彎矩
χy,χz為彎曲屈曲折減系數,彎扭屈曲發生時,應用χTF代替
χLT為側向扭轉屈曲折減系數
NRd為考慮有效截面的軸壓承載力設計值
My,Rd,Mz,Rd為截面彎曲承載力設計值
αy,αz,βy,βz,δy,δz為相互作用公式中的指數,見表6
ωx,y,ωx,z,ωx,LT為與截面位置相關的插值系數,見表7
y-y軸與z-z軸為主軸。
表6 相互作用公式中

表7 插值系數ωx,y與ωx,LT

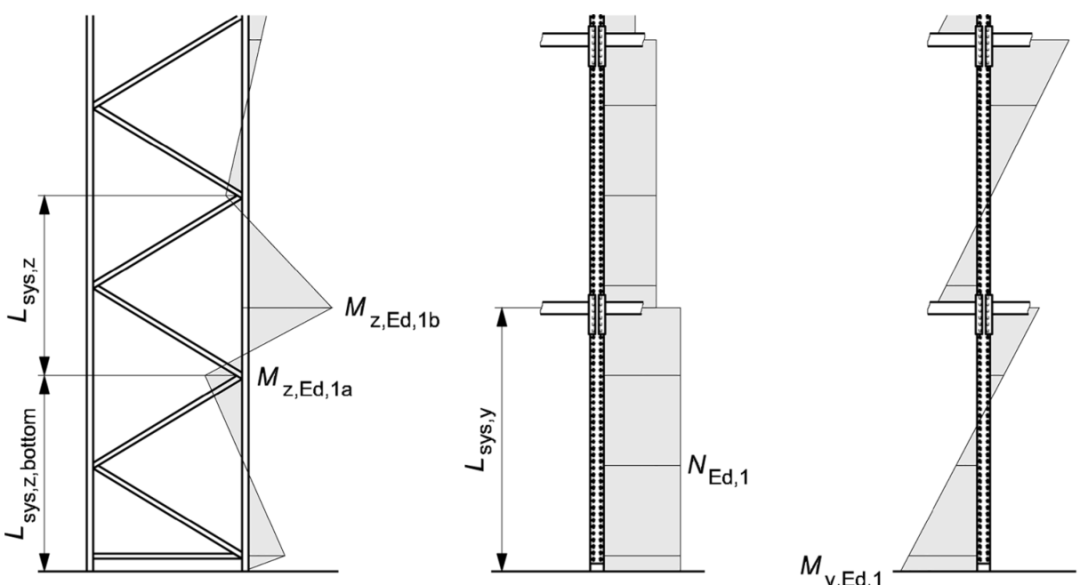
圖7 軸力NEd與彎矩My,Ed,Mz,Ed圖
五、立柱組撐桿的設計
立柱組撐桿及節點除了基于整體分析的內力進行設計外,還需考慮以下情況的荷載最小值:
——立柱組豎向荷載標準值的1.5%
——3kN
該荷載無需與其他荷載或作用組合。
5.1 屈曲長度
屈曲長度系數見表8。
l=KL
lT=KTL
其中
L為立柱組撐桿節點間距離。
表8 K系數
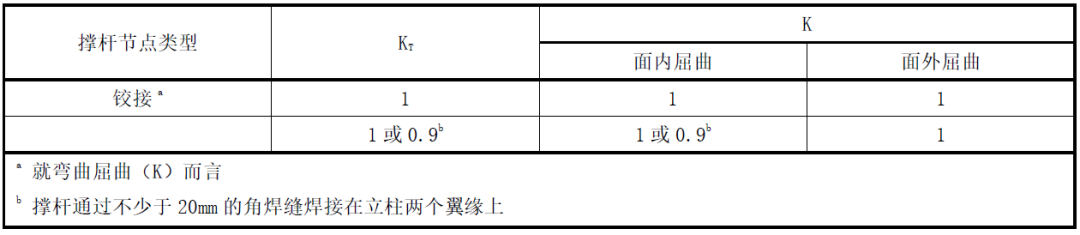
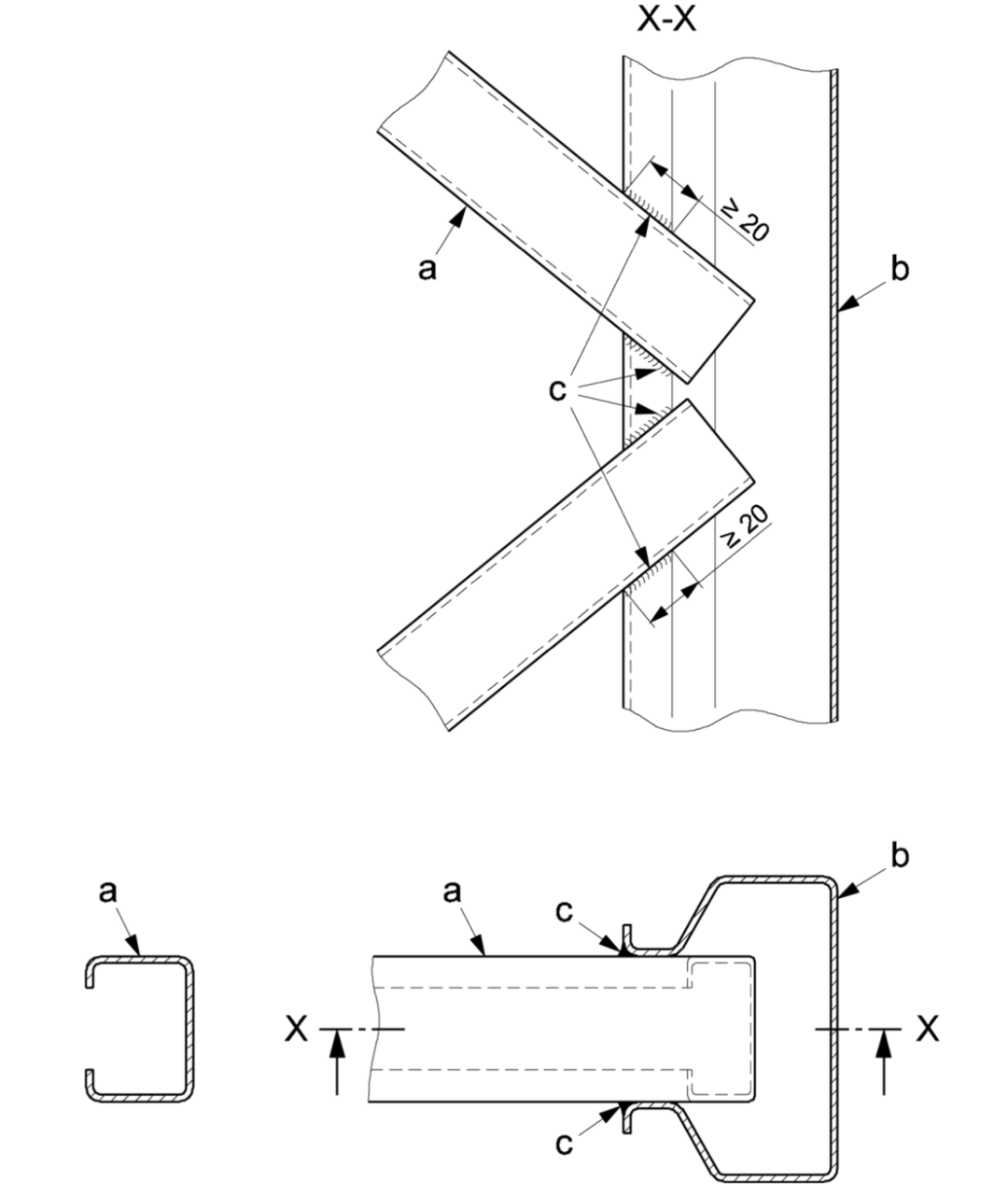
a 立柱組撐桿
b 立柱
c 焊縫
圖8 焊接立柱組撐桿
六、立柱組連桿的設計
對于背靠背貨架,立柱組之間應至少設置兩根連桿。立柱組連桿應位于立柱組撐桿支撐點處,并按照實際情況分布開來。立柱拼接處應額外設置一根連桿。最底部的連桿應設置于地坪以上第二支撐點處。
如果設計中考慮了立柱組連桿,那么立柱組連桿應能抵抗所受到的內力。對于配備叉車的貨架,每根立柱組連桿應能承受至少2.5kN偶然水平荷載引起的拉壓效應。
本站的原創文章,請轉載時務必注明出處:穩圖WESAFE,不尊重原創的行為我們將追究責任。

